Dans un premier temps, pour nous familiariser avec les techniques expérimentales nous avons étudié la microémulsion nue. Grâce à la méthode de FRAPP, nous avions accès au coefficient de diffusion des micelles seules. Nous avons mesuré le coefficient de diffusion en fonction de HC et grâce à l'extrapolation à HC=0, on obtient le rayon hydrodynamique de la micelle.
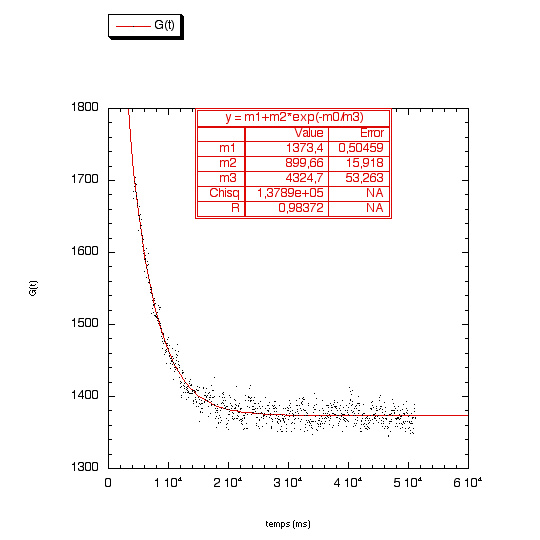
Les données obtenues grâce à la méthode de FRAPP ont été traitées à l'aide du logiciel Kaleidagraph. Celui-ci nous a permis d'ajuster les courbes donnant la fluorescence en fonction du temps. Voici un exemple avec HC=7.5% et i=16 mm:

Ensuite, en faisant des mesures avec des interfranges différentes on a tracé la courbe de l'inverse du temps caractéristique en fonction du vecteur d'onde q qui correspond à q=2p/i. Le temps caractéristique vaut:
t=1/(Dq^2)
Ainsi, pour HC=7.5%, on a:
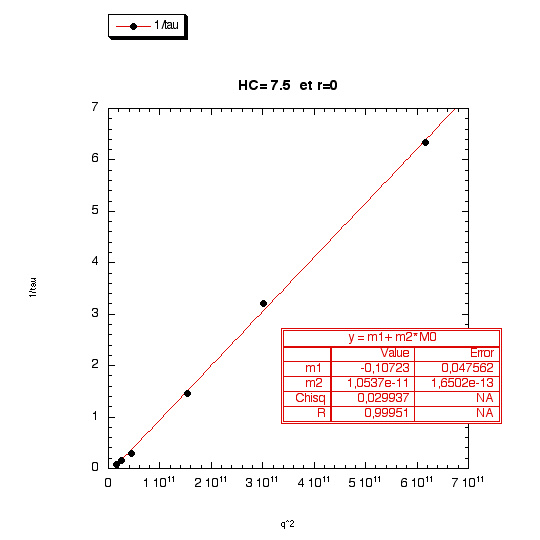
Nous avons ainsi obtenu des droites qui confirmaient la loi vue dans le chapitre 2:
1/t=Dq^2
Nous avons ainsi eu accès au coefficient de diffusion D. Ensuite, en travaillant avec des HC décroissants, nous avons tracé la courbe du coefficient de diffusion en fonction de HC.
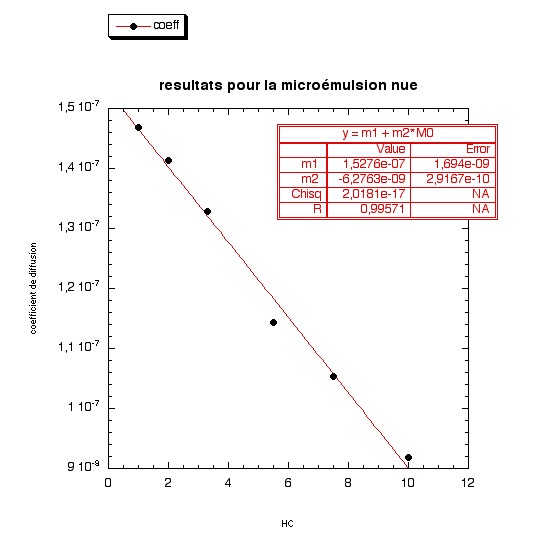
La courbe tracée grâce aux résultats de FRAPP est une droite et elle nous permet d'avoir le coefficient de diffusion à dilution infinie, là où s'applique la formule de Stokes-Einstein. Les expériences réalisées conduisent à un rayon hydrodynamique de 140Å. Or, nous avons vu que les solutions préparées contenaient des micelles dont le rayon avait été ajusté et étudié par diffusion de rayons X aux petits angles. Ce rayon était de 110Å. Une première explication de la différence entre les deux expériences est le contraste des expériences de diffusion de rayons X. En effet, le contraste entre les tÍtes hydrophiles et le c¶ur hydrophobe était trop grand lors de l'expérience, seul le rayon du c¶ur a été mesuré. Si on tient compte du volume des tÍtes, on rajoute 20Å aux mesures effectuées. En fait, la différence restante entre le rayon obtenue par nos expériences et celui prévu vient du fait que les micelles sont solvatées, et donc entourées de molécules d'eau qui augmentent le rayon hydrodynamique.

Représentation schématique de la solvatation d'une micelle
La loi vue dans le chapitre 2 pour ajuster les droites dépendait de F. Or ici, nous travaillons avec HC. En fait, ces données sont proportionnelles donc le coefficient de diffusion obtenue est le mÍme.