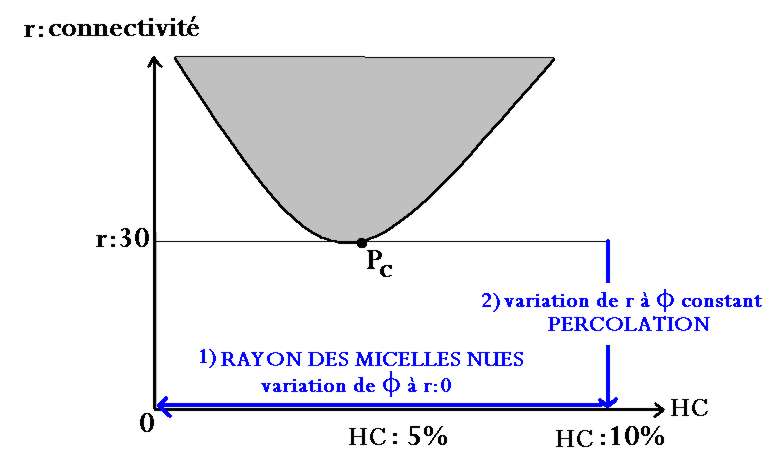
On veut étudier la variation du coefficient de diffusion en fonction de la connectivité pour une concentration en micelles bien déterminée. On se place à HC=10 et on fait varier les connectivités comme le montre le schéma ci-dessous.

On part d'une solution r=30 et HC =10 et on fait varier les connectivités en diluant la solution avec une solution de même concentration en micelles mais sans polymères: c'est la solution HC=10 , r= 0 qu'on on appelle ainsi la solution-mère "nue". Afin d'avoir une bonne précision sur le comportement on étudie donc différentes connectivités en diminuant l'intervalle pour les petites connectivités: on prépare donc les solutions pour HC: 10 et r: 30, 20, 15, 10, 7.5, 5, 4, 3.3, 2.5, 0.
On obtient les résultats suivants:

Coefficient de diffusion en fonction de la connectivité de la solution
On constate tout d'abord l'importance du changement du coefficient de diffusion: entre les connectivités r=0 et r=30, on joue sur un ordre de grandeur. Pour les expériences à connectivité grande (r=20-30) le temps caractéristique était ainsi particulièrement allongé et une expériences pouvait nécessiter une dizaine d'heures d'acquisition. La courbe obtenue montre clairement deux comportements linéaires en D, l'un pour les faibles r et l'autre pour les connectivités plus élevées. Si l'on extrapole ces deux comportements, le point d'intersection nous fournira la connectivité pour laquelle on a un changement de comportement.
On trouve donc une connectivité limite de 7,2 avec une précision de 0.2 dûe à la méthode des droites assez peu précise.
Pour les connectivités r< 6, on a un comportement ``en fleurs'', les micelles ne se pontent pas et les deux têtes des polymères sont plantées dans la même micelle. Pour les connectivités r>10, le système se présente comme un gel connecté. Il paraît donc logique que les mouvements soient beaucoup plus lents c'est -à-dire que le coefficient de diffusion soit beaucoup plus faible. On pourrait penser que les micelles étant connectées, leurs déplacements ne seraient pas suffisants pour être mesurés par la méthode de FRAPP: on mesurerait alors la diffusion de la sonde fluorescente qui quitterait une micelle pour une autre …Mais une telle hypothèse n'est pas valable sinon on aurait le même coefficient de diffusion pour r: 20 et r=30 ce qui n'est pas le cas…On mesure bien le coefficient d'autodiffusion.
On a donc une percolation qu'on peut représenter ci-contre:
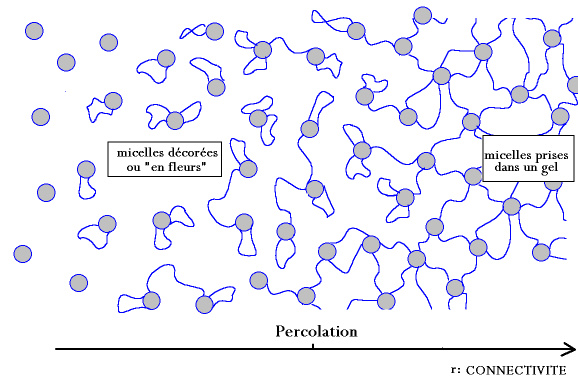
Représentation schématique du phénomène de percolation
Cette transition de percolation est à rapprocher des calculs classiques de percolation, de connectivité limite pour laquelle les polymères connectent deux plaques… Par exemple en prenant en compte 6 voisins pour chaque micelle PG de Gennes a donné une connectivité limite de 4,21 mais notre système compte des premiers voisins plus nombreux [12]. La valeur élevée de notre connectivité de percolation peut s'expliquer par la conjugaison de deux phénomènes:
* Le nombre de proches voisins est supérieur à 6
* La concentration en micelles intervient de manière cruciale.
1) Nous devons compter sur 12 proches voisins:
Selon A.Boutin que nous avons consulté après un cours de simulation moléculaire la structure locale que l'on rencontre dans les liquides est l'icosaèdre, une structure géométrique formée de deux pentagones.
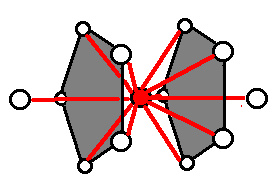
Représentation schématique d'un icosaèdre
Dans ces conditions le nombre de plus proches voisins serait de 12. Cette structure a l'inconvénient de ne pas être extensible et reproductible …Il faudrait donc choisir une structure cristalline qui puisse être périodique dans l'espace, on choisira donc soit la structure hexagonale compacte soit la structure cubique face centrée car ces deux structures ont la compacité maximale de 74% en volume…alors que la cubique centrée n'a une occupation en volume que de 68%. Dans les deux structures de compacité maximale le nombre de premiers proches voisins est de 12… Le calcul serait donc à effectuer dans une structure périodique comptant 12 proches voisins. Il paraît donc normal que la connectivité trouvée soit supérieure à celle pour 6 proches voisins.
2) Influence de la concentration
Dans les calculs de connectivité des plaques, à chaque tête placée dans une micelle correspond une tête dans une autre micelle…dans notre système on peut montrer que plusieurs processus sont nécessaires pour conduire à la connexion de deux micelles…Chaque processus ayant une probabilité inférieure à 1, on devine déjà que la connectivité ``efficace'' pour ponter sera bien inférieure à la connectivité du milieu.